3.7 Strange Attractors

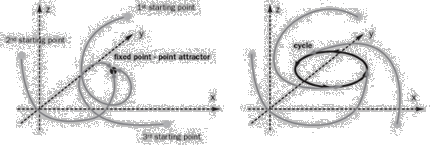
The long-term behavior of a system can be represented in the so-called n-dimensional “phase space”. There the specific time development is described through a trajectory, through which the history of the system is recorded. Attraction areas, to which these trajectories aim, are called attractors. Put into other words an attractor is a preferred position for the system to which it evolves no matter what the starting position is. Once such a position is reached it will then stay on the attractor in the absence of other factors.

The existence of an attractor[01] in general means for a scientific process that it possesses the characteristic either to run in a stable, periodical or quasi-periodical way. ‘Stable’ means that the system aims at a certain end condition, called point attractor or the fixed point of the system. On the other hand a process is ‘periodical’ if it repeats itself through a certain interval of time. Finally ‘quasi-periodical’ means that it lasts some time at the beginning until it turns into a periodical behavior - see picture 21.

Another category of attractors is called strange attractors, whose name arises from their strange characteristics. They consist of an infinite sequence and offer an unpredictable chaotic behavior, but nevertheless in the phase space they occupy a sub-room of lower dimension. Looking at neighboring trajectories their expansions follow completely different directions. From that follows that though the system evolves to and remains on the attractor, it is not possible to give a long-term behavior - see picture 21. This category is often applied to represent chaotic systems[02] .

Footnotes

[01] The word “attractor” originates from the Latin “attrahere”. Voß Herbert, Chaos und Fraktale - selbst programmieren (1994), Franzis-Verlag GmbH Österreich, ISBN 3-7723-7003-9, p.26.
[02] In the geometrical expression a strange attractor is a fractal.