4.2.1 Self-Similarity Dimension "Ds"

The self-similarity dimension “Ds” is equivalent to Mandelbrot's fractal dimension “D”. It proceeds from the fact that in a self-similarity construction there exists a relationship between the scaling factor and the number of smaller pieces that the original construction is divided into[01]. This is true for fractal and non-fractal structures: e.g. a line, as an example for a non-fractal structure, can be divided into three identical parts. In this case the number of new pieces “a” is three and the reduction factor “s” is one third, see picture 23. The dimension “Ds” results from the equation:

a ... number of pieces
s ... reduction factor
Ds ... fractal dimension

  =>
means Ds=1 in the case of a line

Equally a square can be divided into four pieces by using the reducing factor of one half. If the reducing factor is one third then this results in nine similar parts and so on:

Ds=log(a)/log(1/s)=log(4)/log(2)=log(9)/log(3)=2

In general an object is a non-fractal Euclidean structure if there is no growth in length, area or volume as one observes it more closely, which also leads to the conclusion that Euclidean objects always have an integer dimension equal to its topological dimension. In contrast to that, fractal curves are objects that’s fractal dimension is greater than its topological dimension. E.g. the self-similarity dimension Ds of the topological one-dimensional Peano curve is generated by Ds=log(9)/log(1/3)=2. In this case the curve fills the surface it is lying on completely but if only one point is taken off, the curve nevertheless falls apart into two pieces.

The self-similarity dimension of the Koch curve:
 a=4; s=1/3;

 Ds=log(a)/log(1/s)=log(4)/log(3)=1.26186

The dimension can also be measured by using two different scales - scale comparison:

 ... number of pieces of the 1st scale=4
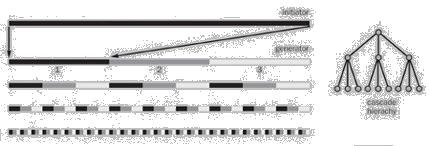
 ... number of pieces of the 2nd scale=16
 ... reduction factor of the 1st scale=1/3
 ... reduction factor of the 2nd scale=1/9
 Ds... fractal dimension measured by the comparison of the 1st and 2nd iteration of the Koch curve.

Footnotes

[01] The smallest “rn” for natural structures also has to be choosen carefully because at one stage the scale of "rn" becomes as small as the scale of the image itself and no increase in length would be observed. This is then called the lower scale of the object.