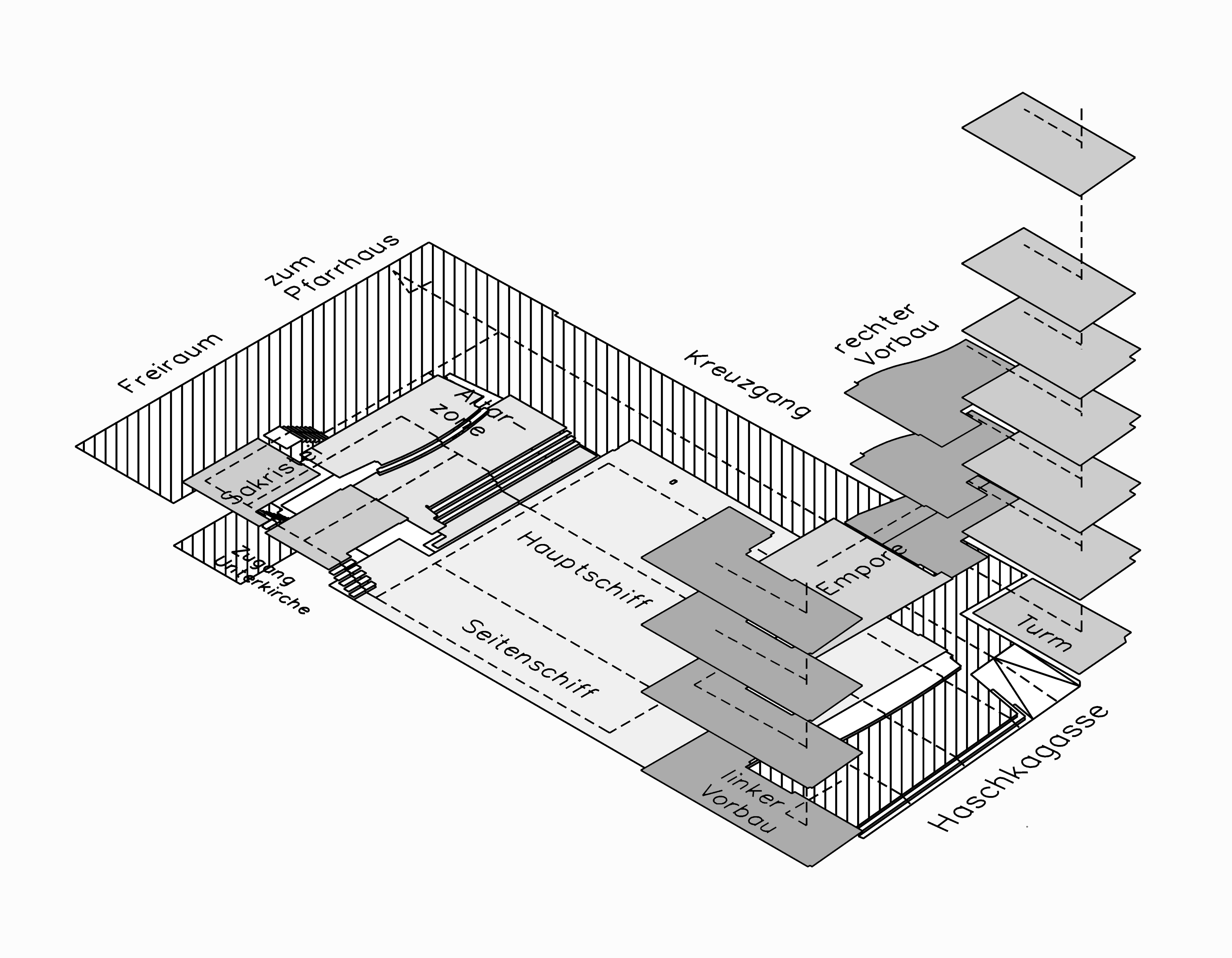
4.2.3 Box-Counting Dimension "Db"

The box-counting dimension “Db” is equivalent to Mandelbrot's fractal dimension “D”. Generally no clearly repeating self-similar structure as in the Koch curve can be found in any real-world object, which means that these less regular shapes cannot be divided into equal parts and by that the self-similarity dimension method will not work. But there is also a problem when measuring the dimension of a coastline or part of it with the help of the measuring-method if surrounding islands are to be included.

In such cases the so-called box-counting method, which is often used by calculating programs for the computer, takes remedial measures. It works very well for images prepared as a black and white image of any object. At the same time it is important to remember that it is the dimension of the image, which is measured, and not the object itself.

How does the box-counting method work? First a grid is put over the image, e.g. a border line or an elevation of a building. Then the boxes, which contain part of this border or edges of the elevation, are marked[01]. The number of boxes of the bottom row of the grid gives the unite-size, the scale. At the next step a lower grid is chosen and again those boxes, which contain a relevant part of the image, are marked. That means by using the box-counting method not the line is divided into parts but the grid, which is put over the line. For calculation the occupied boxes of each grid-size are counted. Finally, as with the measuring-methods above, different scales are compared, see picture 25. The formula for calculating the fractal dimension is the following:

 N ... is the number of boxes in each box-grid which contains part of the structure;
 1/s ... number of boxes across the bottom of the grid - unity-size;

picture 25: The box-counting method

For better comparison once more the example of the coastline of Britain is used. Again surrounding islands are excluded from the measurement, though the box-counting method can include the surrounding islands in contrast to the measuring-method.
The fractal dimension depends on the quality of the map, its scale and the measuring-method. Therefore the same map and the same size as before are used. In the measurement river-deltas are included as far as they could be identified on this scale. This shows another problem. Where is the borderline between the land, river and the sea? The results derived from the measurement are given on the next page.

E.g. the box-counting dimension of the coastline of Britain measured in picture 25 between the scale of 1/s2 and 1/s3 amounts to Db=1.31. The calculated measured dimension “d” for the scale between the unit length of 100km and 50 km is 0.308, that is Db=1.308.

Graphically the box-counting dimension is calculated by transforming the results, marked boxes and the unit-sizes, into a log-log graph. The gradient of the resulting line of the log-log graph is the fractal dimension of the image. But as I will mention later in chapter “7 Problems with Measuring” there are some problems to cope with when using programs, which generate the dimension. Mostly the problems result in a non-straight graph-line. That means that there may be some shortcomings in the original box-sizes of the grids or the quality of the image. Therefore a replacement-line has to be calculated which runs straight. This line is the average of all dimensions given by the log-log graph.

Footnotes

[01] The edges of an elevation may be found around windows, doors, walls, the roof and around certain details, which depend on the scale of the analyzed plan.