5.5.1 The Time

With grand buildings of the past it often took very long time until they were finished. Examples for such architecture are the Cathedral of Chartres, which was finished within about 150 years - second half of 12th century to 13th century -, the Cathedral Notre Dame de Paris - 1163 to 1240 - and St. Peter’s in Rome - 1506 to 1626[01]. Ideas, as in the case of St. Peter’s in Rome, and plans of these buildings were changed and it took a couple of restarts and changeovers during the stage of construction until the buildings were finished. One reason was that the typical architectonical style of the time was influenced by changes in society, political views, problems in economy and other factors. All that and the fact that money was not always available and that the technical possibilities were limited, slowed down the completion. In the course of time many anonymous architects were also on duty and at work, which brought another dimension to it. The cathedral is not the result of the work of one man but the result of the work of many men, of society and of time. Such grand architecture needed a lot of time and changeovers until they developed into the structured interesting buildings, which we can see today, like mountains that are formed by time. Getting a feeling for e.g. the Cathedral of Chartres takes a day, some people even need a week, but finding all details and getting the experience of the history of each part in connection with time takes a life-time[02].

5.5.1.a The Structure

The architect of today of course should not try to rebuild time development, which is not possible either, but maybe he can regard the structure of time as a master builder. E.g. the Cathedral of Chartres consists of sections from Early Gothic to Late Gothic, with some parts being even older and some younger than these periods. What can be built is the character and the structure of such a development, such as the similarity from parts to the whole, the differentiation that nevertheless repeats the characteristics of the whole, which Charles Jencks called the organizing depth. Naturally the cathedrals are only specific architectural tasks, which are more or less restricted to the past, but they show some important characteristics, such as that they are built examples of the influence of time, which brings different styles into an overall concept, they have a rugged surface with elements that are differentiated and repeated on different scales but nevertheless subordinate to the whole, e.g. pointed arches of the Gothic as windows, doors, costal arch and elements of the facade, they have an overall structure which is repeated in sections, e.g. curved waved forms in the floor plan but also in the decoration of the Austrian Rococo, and they are "attractors" for tourists and architecture-theorists, and therefore often published.

5.5.2 Gothic

The pointed rising form of gothic cathedrals reflects the change in religion: before Gothic times there was the imperial view of life "God, emperor, security", which then turned into the view of "purification, cure, uniting"[03].

This philosophy had been translated into the pointed high cathedral that is again reflected and assisted by the pointed arches and gables inside and outside. The period of Gothic can be seen as the first time of international cultural exchange, because of the international participation in the crusades. Men of different regions realized that there were similarities in culture, but also in their national, spiritual and social problems. Therefore the new concepts and forms of the Gothic were propagated in many countries. It was rather the time of an attempt of feeling God - mystic - and of piety than of proving God, as it had been before. The vertical forms of the Gothic helped to come closer to God, to get a feeling for and of God. This shows the complexity of society in the form of its attitude to religion and architecture. Walls became steeper and verticality was also repeated in segments and in details.

5.5.2.a One Style

In addition that the Gothic concept is found in many different variations depending on the region, such as English-, French-, German-Gothic, the time, such as the Early-, Middle- and Late-Gothic, different types caused by cross-section and exposure, such as basilica, basilica with galleries, rung-basilica, hall-church, rung-hall, pseudo-basilica, gallery-hall and pilaster-church, but also on size and usage, such as imperial or clerical. But nevertheless the elements are similar and that can identify them as the Gothic style. This is the concept of fractal geometry, the similarity from the whole, e.g. the Gothic as such or the pointed arch, to its parts, e.g. sub-Gothic-styles or the pointed arch on different scales, see picture 36[04].

There is another interesting relation between society and architectural form, namely that Gothic was the expression of the changes in politics - the rise of France to the greatest power of Europe by a strongly centralized kingdom. At the beginning of the Gothic style the French king had been limited to the Ile-de-France but then the French empire was united and parallel to that Gothic forms were spread around the empire. Through analogy of time and space, the Gothic cathedral had become the visual legitimation of royal domination - the galleries of kings on the facades of coronation cathedrals underline this legitimation[05].

5.5.2.b Fractal Characteristics of the Gothic

The Cathedral of Reims shows self-similarity on different scales, one characteristic of fractals, but with respect to the “true” mathematical fractals in a more abstract way. On the entrance level the five arch-formations are similar to each other but they become smaller from the middle entrance to the outer parts. The straight pointed gable is then repeated in a smaller curved pointed arch beneath, that is then again repeated, but only in the middle three sections. This sequence is found again on the level of the rose windows above in the top-sections of the interspaces. The level above also offers elements that consist of a pointed straight gable with a curved pointed arch beneath, which is then again found inside in the middle section of the sidewalls. Looking at the middle part of the two towers beside the walls, it offers a similar form of the interspaces of the rose window level - two small high vertical cuts, which have pointed arches each, are collected by a pointed arch with a straight pointed gable above, see picture 37.

picture 37: Cathedral of Reims

The tracery of the “Angel Choir” of the Cathedral in Lincoln, Great Britain, also offers the fractal concept of self-similarity. This time the lower level contains eight small but high vertical cuts, formed by the mullions, in each case two together with a quatrefoil crowned by a pointed-arch. In each case such a pointed-arch also holds together two of the remaining four combinations, and finally these two resulting combinations[06]. This means that the fractal concept holds true for three levels, see picture 38.

picture 38: Angel Choir of the Cathedral of Lincoln

Now let’s have a look at the rose windows of the Gothic. The rose window of the Cathedral of Chartres in the lateral axes - 13th century - shows a fractal concept, with the outer form being a circle. This circle is reduced and repeated in the middle part and surrounded by twelve smaller circles. In the outer part of the whole rose window there are again twelve circles that are surrounded by twelve circles each, see picture 39. The window of Mary’s-chapel of the Cathedral of Wells has another structure. In this case a three-pointed curved form is composed similarly to the Sierpinski Gasket, in which the middle part is, however, not taken away. The triangle-shaped object is then repeated on some different scales.

picture 39: Window rose - Chartres

5.5.2.c Ribs and Tree-Branches

In the Gothic style the sequence of “single” rooms of the forerunning Romanesque style has been changed to a unit-room. This has been achieved by surmounting the change of main- and side-pillar of the arcade-zone and the alternating supports respectively, which mostly run into a six-piece vault. For the tendency of reaching great heights, the cross-ribbed-vaulting was used inside to bring the thrust into the pillars that are supported by the buttresses and flying buttresses outside the building. The side-support was needed to catch the shearing forces[07]. - Gaudí improved this concept at the Sagrada Familia by bending the pillars, which made buttresses useless. - In the Gothic style, the ribs of the cross-ribbed-vaulting meet at the pillars, which are often a bundle in continuation of the ribs[08]. It would be interesting if there is a connection between the thickness of the sum of parts in the pillars and the ribs, similar to tree-branches. Leonardo da Vinci wrote that the branches of a tree after a bifurcation are all together as thick as the branch before the bifurcation. That leads to the equation , with being two. That also means that if the thickness of trees is taken into consideration, then trees are not self-similar, because self-similarity demands and a nearly space-filling structure means to have a "D" near the Euclidean dimension of three, see picture 40[09].

picture 40: Leonardo Da Vinci and cross-ribbed-vaulting

5.5.3 Baroque and Rococo

The Baroque style shows the overall structure from the detail up to the building itself in many examples[10]. The round forms of the architecture can be interpreted as the logical development of the shape of a pearl, as the influence of a forerunning element. Because of only one word, pompous or Baroque style itself, a certain impression of the building comes up to mind, though the term style is to be used carefully. In this paper the word style is used as a definition for typical architectural elements and not in the sense of time or defining a period.

So what are the characteristics of the Baroque? One characteristic surely is the strong movement of curved forms in ground plans and elevations, the subordination of all the single elements to the whole - this can be seen as a reference to the fractal character of this style - broken gables and rich decoration[11]. The curved form in ground plans and elevations is also repeated in the decoration itself, which is similar to the character of the Gothic where the pointed arch and verticality are the underlying elements, see picture 41. The Baroque - the time of absolute sovereigns - was the last homogeneous stylistic form. It represents the visible universe but also all that is invisible but strongly sensitive, called the transcendence[12].

picture 41: Baroque - curved elements

The following Rococo was more a style of inner-decoration and less a building style, therefore in this sense the overall concept is mostly reduced to the interior. In "Der große Brockhaus - 1983 - Rococo"[13] the following entry can be found on the Rococo: "... Leitmotif of the Rococo-decoration was the rocaille, an ornament that has been used pictorially in the grotesque-decoration and that had been developed from the asymmetric mannerism image but also from the Baroque Italian mussel-shaped form." This shows on the one hand the development of forerunner-elements that influence the following and on the other hand the importance of a leitmotif as one important aspect for the overall concept. This leitmotif and its variation in scale and position is maybe the reason why some buildings are more interesting than others and seem to be more homogeneous.

5.5.4 Predecessor Buildings

5.5.4.a Chartres

"Baedekers travel guide-book France"[14] writes about the Cathedral of Chartres: "After awful fires - in 743, 858, 1020 and 1194 - of the older churches, which had eventually been built on a Gallic-Roman holy shrine, most parts of the house of God were rebuilt between 1195 and 1220." - Many buildings of the past can be found which were built on the site and/or the foundations of older ones, sometimes because of religious or political reasons and sometimes because of economical ones. One example is the main building of Schönbrunn Palace that used parts of the foundations of the predecessor building, the so-called “Katterburg”. The place and the building are formed together; the predecessor building influences the new one in size and dimension of construction. - Back again to the Cathedral of Chartres: "The facade had been built between 1140 and 1160 in the strong forms of the Early Gothic and was not hurt by the fire of 1194. ... The steeple in the south, finished in 1170, is an example of the rich stylish Gothic. The north steeple got an additional finish between 1507 and 1513. ..." This describes the richness of different styles within one style - strong Gothic and rich stylish Gothic -, which also means that a couple of centuries are represented in this cathedral as in many others too. But the building is nevertheless seen as a whole and not as a jumbled together mass of different parts.

5.5.4.b Templo Expiatorio de la Sagrada Familia in Barcelona

One of today's examples of a big cathedral-building site is that of the Templo Expiatorio de la Sagrada Familia in Barcelona by Antonio Gaudí, who became supervisor of the building works in 1883. The original plans by Villar intended a rigorous Neo Gothic cathedral whose crypt had already been dug out and the columns for the apse had been started. That means that Gaudí also depended on a predecessor building, and so he for example could not change the axis of the cathedral nor could he change the number and the look of the columns, as he would have done otherwise. Antonio Gaudí interpreted the Gothic form of a cathedral in a new way, by cleaning the Gothic of all superfluous shapes or by further developing the forms, and thus overcame historism, e.g. he maintained the Gothic windows but he added different segments of a circle for balance.

The facade looks like a big sculptured book with scenes and symbols from the Bible, of Catholicism. A “building-algorithm” can be expressed through the rule: show scenes of the Bible using a certain scale and position, at which upper ones should be presented bigger. The position e.g. can be defined by the importance of the scenes or chronologically: Gaudí separated the scenes of Christ on earth, Christ as the liberator and Christ as the judge of life and death on the three main facades.
The number of twelve towers is a symbol for the twelve apostles, and the upper parts of the towers look like miters as a symbol for the development of bishops out of the apostles. They are built in the form of rotational paraboloids and not in "Gothic pointed forms". Seven chapels are placed around the altar in a fan shaped way; the altar is the center like a point attractor. In addition to that he cleaned the altar from all decorations, which in former times, such as in Gothic times, almost made it disappear.

Antonio Gaudí further developed the construction of buttresses and arches of the Gothic and improved the static - he used e.g. catenarian-models and cable-models with sandbags that showed the reverted interrelation of forces. He did not like the huge buttresses of the Gothic as we find them in the Cathedral of Cologne and therefore he used sloping pillars in connection with parabolic arches. These forms look like trees in a forest, an analogy to nature and also to fractal geometry? The column is no longer just a vertical straight cylindrical Euclidean form but it follows the same rules as a tree that is formed by weather, from stem to branch and to the widely ramified boughs. Antonio Gaudí not only brought nature into ornamental forms like the designers and architects of the Art Nouveau but he also used the construction principles of nature, its underlying structure, e.g. the interrelations of the forces of a tree. This can be one interpretation of fractal geometry in architecture; fractal nature is brought into architecture by construction and not only as a decorative element on the surface. "Fractal form follows natural construction", the surface is influenced by its underlying structure, see picture 42.

picture 42: Sagrada Familia

Antonio Gaudí thought of a flat piece of iron, which had to be formed into a three-dimensional object by the smith, he formed the whole out of a flat ground. Mies van der Rohe on the other hand built with flat straight elements, which is a completely contrary way of architectural thinking.

The Sagrada familia is built in the spirit of the Gothic with the influence and a new interpretation prevailing at the turn of the century. Up to now it has been a building site for over a hundred years, mainly for the 20th century, and according to Gaudí its completion will still last a long time period which will bring up different styles, construction-methods, materials and forms, but all based on the underlying idea of Gaudí’s handed down models and sketches. In this sense after the death of Antonio Gaudí in the year 1926, reinforced concrete, as a new development, was used for the floor construction[15].

5.5.5 Modern

In "Fractal Geometry in Architecture and Design" Carl Bovill measured the fractal dimension of a cubist painting by Le Corbusier and wanted to show by that the lack of interesting detail from a certain scale onwards in modern paintings and buildings.

Is there any connection between purism and nature and if yes where is it to be found? Put very briefly, cubism believed that objects constructed, built and made by man are tested for their fitness of purpose as it is done in nature. In this sense the same laws of economy and fitness as those found in nature test these objects. The result of this is that there is a basic rule that leads to general harmony and order. So the reduction to primary Euclidean shapes and basic colors was an attempt to show the “basic natural laws”. But as Bovill’s measurements illustrate these natural basic laws were only translated into paintings and buildings up to a certain scale.

5.5.5.a Le Corbusier - Purism

According to Bovill[16] Le Corbusier's painting “Nature Morte à la Pile Dassiettes” for example has a fractal dimension of 1.53 on a scale between 1/13 and 1/26 of image size, which is quite similar to fractal dimensions found in natural forms. Looking more closely the painting becomes less interesting and the dimension between the scale of 1/52 and 1/104 is only 1.14 - D(26-52)=1.28 -, which means that on this scale-range there is an obvious lack of details. This also shows us that for purism the influences of man-made machines seemed to be much higher than those of the principles of nature. That may be the reason for the limited range of scale, on which natural fractal dimension is presented. In contrast to that, Wright got deeper into the structure of nature and thus brought details into his buildings, which lead to similar fractal dimensions even up to small scales - for my own measurement of the same painting but between different scales see picture 43.

picture 43: Le Corbusier

Nature Morte à la Pile D’assiettes

D(13-26)=(log300-log104)/(log26-log13)=1.528; 
D(26-52)=(log726-log300)/(log52-log26)=1.275;
D(52-104)=(log1604-log726)/(log104-log52)=1.144;

the results of the measurement by Bovill: D(13-26)=1.53; D(26-52)=1.12;

The same phenomenon can be found at the “Villa Savoye” by Le Corbusier, a so-called "machine for living". This is an example for man-made or man-constructed geometry in contrast to natural geometry as it is represented by fractals. The dimension of this building, measured for a scale-range of 1/16 to 1/32, results in 1.42, that for a scale between 1/32 and 1/64 in 1.33. This means that the building does not reach the Euclidean shape as quickly as the painting. But looking even more closely on a scale of the window-strips, the dimension drops to 1.0 - D(64-128)=1.17! That means that from a certain scale onwards there is a lack of detail and the dimension turns to Euclidean geometry[17]. What is missing then is the natural, structured depth, see picture 44.

picture 44: Le Corbusier - Villa Savoye

D(16-32)=(log308-log115)/(log32-log16)=1.42; 
D(32-64)=(log773-log308)/(log64-log32)=1.33;
D(64-128)=1.17

the results of the measurement by Bovill: D(14-28)=1.42; D(28-56)=1.33;

5.5.5.b Nature and Construction

The differences between Frank Lloyd Wright and Le Corbusier can be found in their different basic understandings of constructions. Le Corbusier used and looked for materials and forms from man-made machines, from industry. He believed in the strength of the “laws of efficiency and fitness in nature” and translated that concept into his buildings. Frank Lloyd Wright on the other hand believed in the development of natural materials, the former translation into architectural motifs, and their development up to now. By using natural materials in a way nature does, complexity and order are produced. As the IFS-method depends on the rule and not on the starting image, the same is true for the differences between Le Corbusier and Frank Lloyd Wright. The rules defining how materials have to be used, in a natural or industrial way, are important not the starting material or program.

Beside that Le Corbusier also used the idea of connecting and relating parts of the facade by an overall idea, which has been said to be a fractal concept. The elevation of Ozenfant's studio for example is constructed by a rule of transformation that is used for the whole facade and even for the proportions of the windows, see picture 45.

picture 45: Le Corbusier - Ozenfant’s studio:

The transformations used are similar to those of the Iteration Function Systems - see chapter "3.3 IFS - Iteration Function Systems".

The images show the layout of the front elevation of Ozenfant’s studio.
The diagonal through the whole front determines the subdivision of the windows. Thus the rectangles of the windows are similar to the whole.

5.5.5.c Euclidean and Fractal Concepts

If we call the modern style more Euclidean-like, the overall concept is meant, the rectangular walls and the cubical forms that refer to Euclidean geometry. This concept comes up by zooming closer to the object, because then it really turns into Euclidean forms, the dimension turns to one.

Nature has an organizing depth and this is what really makes it fascinating from the large to the small. In comparison to architecture this is also the concept that makes Gothic cathedrals, rural houses and some of the so-called organic architecture so interesting and diversified. Naturally this is only a generalization and of cause there are exceptions as some villages with smooth rural houses - which have to be looked at in connection with their surroundings and with the materials available - or the church Notre-Dame-du-Haut in Ronchomp by Le Corbusier - where walls and roofs are hollow concrete shells and the whole building has a plastical bodily effect, which is a contrast to the rectangular Euclidean style of the “other” Le Corbusier -, but mostly this statement is true. "Good" architecture lies between the smooth Euclidean and a too complicated geometry and can be characterized as deterministic chaos that is brought into shape by fractals. Too much complexity leads to non-understandable architecture with very high fractal dimensions.

5.5.5.d De Stijl

De Stijl, as an example for modern architecture, demanded "measure and number, clearness and order, standardization and production in quantity, perfection and best realization"[18]. It was the style of interpretation and realization of the geometric abstraction of Piet Mondrian - the concrete painting - in cubist architecture. Each surface corresponds to a certain part of the house such as piers and windows, which are arranged in differently deep spaces. This is the Euclidean way: differentiation of the "vocabulary" of the building in space, construction and segments.

5.5.5.e Conclusion

Overstressing the unity, the "overall-society" builds for the masses only, which was also true for the modernists who only built for the middle class without looking at the different layers of society. In the modern style of the 1920ies, the angles of buildings had to be rectangular and their facades had to be smooth, white painted surfaces. If we regard our homes as our third skin, it seems that we cannot think of such house-types, because a skin is something organic, nature-like and not a sterile, rectangular Euclidean thing. That made Gropius say we had to wait until moss comes up and man lives in those white modern buildings, because then the smooth surfaces turn to life[19].

Society can be shown through infinite possible variations and combinations of parts of society, which are then integrated into the character of buildings - as a mirror of time. Following from that democracy is not achieved by standardization but by variation and by showing all parts in the right combination.

5.5.6 Organic Architecture

Organic architecture as such has never really been defined, but what it mostly stands for is the inspiration or the underlying structure that is used for construction or form of buildings. Materials for architectural constructions come from nature and by that are used as architectural motifs, e.g. the Egyptian columns in form of papyrus plants, see picture 46. In this sense forms have been developed up to now. But mostly it is rather the concept than the form that we look for in nature. Abstract steel-"tree-twigs" as constructive columns, shell constructions from the inspiration by sea urchins may therefore also belong to organic architecture.

picture 46: Translations

left: Acanthus and - capital/ middle: Papyrus and - capital ~1450 B.C.
right: Papyrus column ~ 2675 B.C./ Bundled papyrus column ~ 1500 B.C.

5.5.6.a Frank Lloyd Wright

The organic architecture tried to achieve harmony between architecture and landscape. Its origin lay in the Art Nouveau that orientated itself on the biological knowledge of the 19th century. Frank Lloyd Wright was one of the most famous representatives of organic architecture. Proceeding from the principle of Sullivan to develop a plan from inside to outside, Frank Lloyd Wright built organic houses that grew out of the conditions of the environment with regard to purpose, material and construction[20]. The most important examples are the so-called prairie-houses where he brought nature and man-made architecture in harmony. Some characteristics of this kind of dwellings are the low extensive ground plans, through which the function determines size and position of rooms. The hall, eating place and living room are no longer separated but flow into each other, rooms rise out of the center and determine the outside, flat cubes are connected with nature by large overlapping, gently sloping, roofs - influences from Japan -, terraces and gardens go together, the chimneys are heavy-set and the materials timber and stone are used. The elements of the building are strictly constructed out of the architectural function and are not covered in any way, see picture 47.

picture 47: Frank Lloyd Wright - prairie houses.

Overhanging roof , horizontal organization of the facade, band of fenestration, facade-facing bricks, hip-roof.

above: 1909, Robie house, at Chicago
below: 1906, Darwin Martin house, Buffalo

5.5.6.b Structural Similarity

Thinking of concrete shells and similar examples there is something missing if we want to call them organic architecture. When Frank Lloyd Wright called for inspiration from nature he did not copy nature but translated it into architecture. What he was looking for was the importance of a simple, specific form, which would be the expression of the building. From this basic idea and basic form the whole and all other formal elements are derived which means that the formal elements are held together in scale and character - complex forms are developed out of basic rules or ideas where smaller parts are the "mirror" of the whole[21].

Like in the case of fractals, which are generated by certain simple rules, these rules are changed to a basic idea, a simple, specific, single form that runs through iterations. The more elaborate details can be found, the more iterations are used in the building. In Robie house by Frank Lloyd Wright for example the cascade of interesting detail comes down to the stained glass designs of the windows, see picture 48. If only a few iterations of the idea are brought into a building, the character may be the same but only up to a certain scale - from then on it will become smooth. Beside that, as there exist different algorithms for different types of trees, clouds and other natural forms, which means that there is not only one rule for all organic forms, the same is true for architectural concepts, which cannot be reduced to only one rule, either.

picture 48: Frank Lloyd Wright - Robie house.

grid size = 1/8 and grid size = 1/32; grid size = 1/16 and grid size = 1/64

Robie house - D(slope 8-64)=1.57: D(8-16)=1.64; D(16-32)=1.55; D(32-64)=1.54;
the results of the measurement by Bovill: D(24’-12’)=1.645; D(12’-6’)=1.485; D(6’-3’)=1.441;

grid size = 1/10, 1/20 and 1/40

stained glass window - D(slope 5-40)=1.56: D(10-20)=1.65; D(20-40)=1.66;
the results of the measurement by Bovill: D(6’’-3’’)=1.721; D(3’’-1.5’’)=1.626;

5.5.6.c The “Unity Temple”

When Frank Lloyd Wright called for the underlying structure of nature in design, he for example thought of the canopy of a wood. This is true for the idea of “Unity Temple” where he thought of the light that is filtered through a forest with a complex form in the upper regions, the branching zone, simpler forms at the trunk zone and again more complexity at the root stage on the ground, with the leaves lying there. The fractal box counting method can also measure this similarity between the canopy of a wood and the "Unity Temple". Thus the fractal dimension - measured by Bovill - of the upper part turns out to be about 1.42, that of the middle part about 1.22 and the lower part 1.67 - for all three measurements the scale-range is defined between 7.5 and 3.7 feet.

In "Fractal Geometry"[22], Carl Bovill compared the Robie house with the "Unity Temple" - see also other examples for a temple on picture 49. His result for the dimension of the Robie house between the scale-range of 12 and 6 feet, measured with the box-counting method, is 1.485, that of the “Unity Temple”, between the scale-range 7.5 and 3.7 feet, 1.482. This shows that the underlying structures are similar, but of course the forms are certainly different.

picture 49: Frank Lloyd Wright - "Unity Temple".

whole temple: D(13-26)=(log216-log71)/(log26-log13)=1.605; D(26-52)=1.549; D(52-104)=1.386;
the results of the measurement by Bovill: D(15’-7.5’)=1.621; D(7.5’-3.7’)=1.482;

upper part of the temple: D(13-26)=1.46; D(26-52)=1.51;
Bovill: D(7.5’-3.7’)=1.42;

middle part temple: D(13-26)=1.42; D(26-52)=1.06;
Bovill: D(7.5’-3.7’)=1.22;

lower part of the temple: D(13-26)=1.90; D(26-52)=1.71;
Bovill: D(7.5’-3.7’)=1.68;

some temples

Different kinds of temples for comparison
On the following pages some examples of ancient temples are given - e.g. the treasure house in Delphi, a Doric temple in Syracuse, a Doric temple in general and the Erechteon in Athens. The tables below the pictures give the results of the box counting method such as the number of boxes that were hidden by the box-counting method, the log-log results and the fractal dimension between two certain scales. The dimension on top of the tables shows the overall fractal dimension that was measured with the computer program “Benoit”. At the end of this entry concerning picture 53 all examples are compared by their dimensions and some conclusions are given.

1st antique example: "The treasure-house of the Athens in Delphi"

The lower part of the treasure-house of the Athens in Delphi can be identified as the smooth, line-like part of the temple. First the stairs are similar to a plane - Db of the 2nd stage=1.93 - which then turn very quickly to a one-dim. line - so this part does not offer many details at different scales.

2nd antique example: "A Doric temple in Syracuse"

The whole elevation of the Doric temple in Syracuse remains on a high fractal dimension, from the distance - about 1.71 - to the nearness - about 1.63. The same holds true for the upper and middle part of the temple with fractal dimensions between 1.62 and 1.74. From this follows that coming closer - different scales - there are always new elements, details, that come into attention - in the upper part, the gable, these are e.g. the triglyphs, in the middle part the fluting of the columns. In contrast to that the lower part decreases very fast from 2.0 to 1.38.

3rd antique example: "A temple of Doric temple in general"

4th antique example: "A temple of Ionic order in Athens - the Erechteion"

The picture on the right side shows the surface of the computer program “Benoit”. On the left half the line of the log-log curve is printed, whose slope stands for the fractal dimension of the image - the white lines of the picture being counted as shown on the right lower half of the surface. As one can see, the points of the log-log-curve are all lying on the “replacing-curve” - the slope -, which means that the object is obviously a fractal with self-similar patterns. The starting scale can be changed in the field called “side-length of the largest box” - in the example of the Erechteion that is 157 pixels - and the reduction of the box-size is determined by the “coefficient of the box-size decrease”.

The middle part of the “treasure-house of the Athens in Delphi” and the “Doric temple in general” show similar fractal dimensions between 1.43 and 1.47 - except D(s1-s2) of the latter - with a “slope” of 1.45 and 1.53 respectively. So these two examples are not only visually similar - big entrance in the middle, two columns with fluting, “simple” capitals - but also in their fractal dimensions. The lower parts of these two examples differ a little bit more. The “Doric temple in general” has a higher fractal dimension D(slope)=1.74 in contrast to 1.29 of the “treasure house”. One reason for that may derive from the smaller heights of the stairs of the first example, so that more boxes are hidden from stage to stage.

The stocky Doric temple in Syracuse has a higher fractal dimension - Db=1.687 - than the “treasure-house of the Athens in Delphi” - Db=1.49 - and the “Doric temple in general” - Db=1.61. This results from three facts: 1st) the upper part - D(slope)=1.675 - shows more details around the gable - sima and corona are more elaborated -, 2nd) the middle part - D(slope)=1.672, which is much higher than for the examples before -, consisting of the columns, is smaller, the columns themselves are wider, the distances between them are smaller and the outer ones also have flutings, and 3rd) the lower part shows the outline of the single stones - D(slope)=1.796.

In the first three examples the fractal dimension of the upper part increases when the triglyphs attract our attention, this is mainly at a distance from 1/52 to 1/104. From this follows that the details of these elements come into attention in the later stages: they continually give additional information from the large to the small; there is always something that could not be identified in the stage before. Besides the upper part of the “Doric temple in general” has acroterions, that is sculptures, which also have some influence on the fractal dimension - Db increases from 1.585 to 1.697.

The fractal dimension of the Erechteion in Athens remains high from 1.78 over 1.74 to 1.60, which derives from the richness of details. In all parts more and more information can be found from the asymmetrical whole, the frieze, the Ionic columns, the Antefix, the Caryatids to the outline of the wall.example: "A temple of Ionic order in Athens - the Erechteion"

5.5.6.d Eero Saarinen

In "Architekten - Begegnungen 1956-1986"[23] Helmut Borcherdt repeats parts of a lecture of the architect Eero Saarinen in Munich of 25th October 1960. The contents of this quotation are the planning of his own new house, which could not be built because of his death one year later. The building-site was a densely wooded, rocky bank of a river. - From the point of view that buildings, which take up the structure of the environment, have a fractal dimension similar to that, this building-site would cry for a higher dimension. This is because fractal dimension is the measurement of roughness or detail-richness. - In Eero Saarinen’s opinion the surroundings would ask for an unconstrained, dark romantic building - of high dimension. As Saarinen had mentioned at the beginning of his lecture about architecture as a whole, this suggested that the romantic unconstraint element had to be maintained in the inner parts.

In this connection he had to solve the problem that on the one hand he wanted to create the building as a unit and on the other hand with the right transition from a wild romantic outward appearance to a more formal interior. This is the leitmotif, but the interior design of the rooms had not been solved. The inner parts that are characterized by Saarinen's lifestyle would not be that unconstrained, which means that the overall concept had to be transferred by another rule or, better to say, adjusted. This is quite similar to the modified structure in other concepts of e.g. the competition for the opera in Cardiff by Greg Lynn, where an overall concept has been modified in parts by outer influences that nevertheless fit into the whole.

5.5.7 Contemporary

One category of “new architecture” is the "land-form" - earth art - architecture as it is mentioned in “Arch+ number 141”[24]. Under the headline of “computer architecture” we find a development of computer generated buildings that take up mathematical theories - such as folds, fractals, chaos, complexity, algorithms - and translate them into architecture, see picture 50. “Land-form“ architecture stands in correlation with the theory of complexity, but also with cosmology and non-linearity. It is also an attempt of achieving harmony between modern architecture and the city. This kind of architecture wants to be in competition and correspondence with man-made and with natural environment. Most of other modern architecture in cities is monumental, crushing or uses stereotypes - architecture as articulated landscape.

picture 50: Peter Eisenman

Department of Art, Architecture and Planning, University of Cincinnati (1992-95).

The new building mediates between the waves of the landscape and the zig-zag rectangles of the existing school - forming a middle part of mixture.

5.5.7.a Zvi Hecker

Out of metaphors the Israeli architect Zvi Hecker developed a "land-form" building, the Jewish school "Galinski-Schule" in Berlin. The overall geometry is taken from a sunflower, which connects snake-shaped corridors, mountain-stairs and fish-shaped rooms. The sunflower is placed in the center of the object, representing the heart of the school - a circle-shaped lawn -, while the fish-shaped parts are grouped around. The reason why it is nevertheless not a pressed constructed pure formalistic building lies in the two other systems: one is a rectangular grid, as the “man-made part”, and the other is a concentric circle that is put over the sunflower. This results in self-similar but not identical rooms. Through the sunflower form the architect was able to let the existing trees around survive, which is correspondence with environment, see picture 51. Another positive aspect is that of urbaneness, which is reached by small, curved streets and paths, similar to a historical city, where shapes and places have been formed at random and by history[25].

picture 51: Zwi Hecker - Galinski school/Berlin.

The complexity is produced by the overlapping of different constructional systems, which makes orientation more difficult than in simple logical systems with only one grid. To get a better orientation in the complex form and for construction, the particular parts have been painted differently, so the three geometric systems are pink, green and blue. That makes the complexity of the building readable, which is often found in "land-form" architecture. In many examples of similar buildings simple materials, simple forms and abstraction produce complexity like in the Jewish school "Galinski-Schule" in Berlin. This is once more the concept of fractal geometry: to get a complex object out of simple rules or algorithms. This may be the difference to "modern-architecture": complexity in contrast to simplicity.

5.5.7.b Greg Lynn

The contribution for the competition for the opera in Cardiff by Greg Lynn shows on the one hand the use of self-similar, true mathematical fractals and on the other hand the interpretation of symmetry by Bateson - see chapter "5.4.1 Symmetry and Mutation". The fractal-form was developed out of the form of the oval harbor-basin next to the building-site. The coastline had been analyzed for self-similar patterns that were found in inlets of bays, rivers and harbors along the coastline. This "catching" of water by land was used as the concept of the surroundings. The fractal generated out of that has its origin in an oval that is copied to the right side by 45 degrees with a certain reduction-factor and to the left by 90 degrees with another reduction-factor. A new arrangement was made because of the demands of an opera, like the connection of foyer, stage, cloakroom and shops. This system was then modified and controlled by general information from the context, with the ovals being rotated, tipped out and arranged in the way that they could be connected with surrounding roads, building-walls and views. The environment mutated the fractal with higher symmetry, according to Batesons' theory. The resulting form has new, additional inlets of the coastline[26].

5.5.7.c Bernard Tschumi

The Parc de la Villette in Paris represents an example for “deconstruction”. For that concept Tschumi divided the whole program into pieces. These pieces were then placed on a grid. The resulting structure consists of point attractors, straight galleries and random curved promenades. These three parts together result in a complex structure that has no starting and ending and no defined boundaries as it is true for the Julia sets, see picture 52. In general fractals do have a beginning but no ending, because of infinity iterations - zooming into the border of the Julia sets means to find more and more complexity[27].

picture 52: Bernard Tschumi - Parc la Vilette/Paris.

The images above show various organizational types - bands of planning, confetti of small furniture, circulation and existing buildings.<//font>

Footnotes

[01] Koch Wilfried, Baustilkunde - Das große Standardwerk zur europäischen Baukunst von der Antike bis zur Gegenwart, Mosaik Verlag, p. 157, p. 168, p. 227.
[02] Toman Rolf, Die Kunst der Gotik (1998),Könemann, ISBN 3-89508-313-5.
[03] Koch Wilfried, Baustilkunde - Das große Standardwerk zur europäischen Baukunst von der Antike bis zur Gegenwart, Mosaik Verlag, p.148.
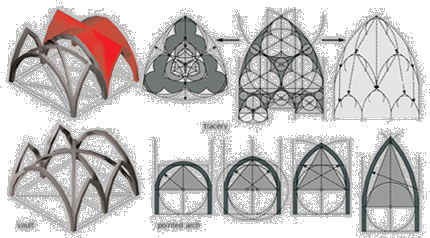
[04] The word Gothic arises from the Italian "gotico", which means barbarian, not-antique. The architectural expression of the Gothic style is the pointed arch and the buttress with ribbed vault. Though both elements have been used in the Romanesque style before - the pointed-arch has its origin in the Islamic world - only then they have been favored before the many other known elements. Koch Wilfried, Baustilkunde - Das große Standardwerk zur europäischen Baukunst von der Antike bis zur Gegenwart, Mosaik Verlag, p. 157, p. 168, p. 149.
[05] Koch Wilfried, Baustilkunde - Das große Standardwerk zur europäischen Baukunst von der Antike bis zur Gegenwart, Mosaik Verlag, p.149.
[06] Toman Rolf, Die Kunst der Gotik (1998),Könemann, ISBN 3-89508-313-5, p. 139.
[07] Koch Wilfried, Baustilkunde - Das große Standardwerk zur europäischen Baukunst von der Antike bis zur Gegenwart, Mosaik Verlag, p. 157, p. 168, p. 149.
[08] Brockhaus, Der große Brockhaus Kompaktausgabe in 26 Bd., Band 8 Gasthörer bis Grimaud (1983) aktualisierte 18. Auflage, F.A. Brockhaus Wiesbaden, p.309.
[09] "D" is called the diameter-exponent. Mandelbrot Benoit B., Dr. Zähle Ulrich (editor of the German edition), Die fraktale Geometrie der Natur (1991) einmalige Sonderausgabe, Birkhäuser Verlag Berlin, ISBN 3-7643-2646-8, p.169.
[10] For a long time Baroque meant pompous, which was also brought into literature and music - sometimes the word "overloaded" can be added.
[11] Brockhaus, Der große Brockhaus Kompaktausgabe in 26 Bd., Band 2 Archi bis Belgien (1983) aktualisierte 18. Auflage, F.A. Brockhaus Wiesbaden, p.294.
[12] Koch Wilfried, Baustilkunde - Das große Standardwerk zur europäischen Baukunst von der Antike bis zur Gegenwart, Mosaik Verlag, p. 157, p. 168, p. 237.
[13] Brockhaus, Der große Brockhaus Kompaktausgabe in 26 Bd., Band 18 Ratenwechsel bis Safanija (1983) aktualisierte 18. Auflage, F.A. Brockhaus Wiesbaden, p.243.
The Portuese word "barocco" means "little stone, irregular, sloping-round pearl" which indicates the origin in the artwork of jewellers.
[14] Baedecker, Frankreich (1988) 4. Auflage, Karl Baedecker GmbH Deutschland.
[15] Zerbst Rainer, Antoni Gaudí (1993), Benedikt Taschen Verlag GmbH, ISBN 3-8228-0067-8, p.190.
[16] Bovill Carl, Fractal Geometry in Architecture and Design (1996), Birkhäuser Bosten, ISBN 3-7643-3795-8, p.139.
[17] Bovill Carl, Fractal Geometry in Architecture and Design (1996), Birkhäuser Bosten, ISBN 3-7643-3795-8, p.141.
[18] Koch Wilfried, Baustilkunde - Das große Standardwerk zur europäischen Baukunst von der Antike bis zur Gegenwart, quotation by Theo van Doesburg in the year 1924, Mosaik Verlag, p.386.
[19] Jencks Charles, Die Architektur des springenden Universums, Arch+ number 141 (1998), Arch+ Verlag GmbH Aachen, ISSN 0587-3452, p.66.
[20] Brockhaus, Der große Brockhaus Kompaktausgabe in 26 Bd., Band 24 Weltkrieg bis ZZ (1983) aktualisierte 18. Auflage, F.A. Brockhaus Wiesbaden, p.182.
[21] Bovill Carl, Fractal Geometry in Architecture and Design (1996), Birkhäuser Bosten, ISBN 3-7643-3795-8, p.127/128.
In general nature should not be imitated but the structure should be found and brought into architecture. This structure is called the fractal concept, a basic idea on every scale, the variation of a theme, idea and rule, the identification of parts and the whole, no strict symmetry.
[22] Bovill Carl, Fractal Geometry in Architecture and Design (1996), Birkhäuser Bosten, ISBN 3-7643-3795-8, p.130.
[23] Borcherdt Helmut, Architekten - Begegnungen 1956-1986 (1988), Georg Müller Verlag GmbH, ISBN 3-78844-2181-4, p.89.
[24] Jencks Charles, Die Architektur des springenden Universums, Arch+ number 141 (1998), Arch+ Verlag GmbH Aachen, ISSN 0587-3452, p.106.
[25] Jencks Charles, Die Architektur des springenden Universums, Arch+ number 141 (1998), Arch+ Verlag GmbH Aachen, ISSN 0587-3452, p.106.
[26] Lynn Greg, Das erneuerte Neue der Symmetrie, Arch+ number 128 (1995), Arch+ Verlag GmbH Aachen, ISSN 0587-3452, p.48.
[27] Bovill Carl, Fractal Geometry in Architecture and Design (1996), Birkhäuser Bosten, ISBN 3-7643-3795-8, p.175-177.